Merge Sort
Merge Sort in C
In computer science, merge sort (also commonly spelled mergesort) is an efficient, general-purpose, comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the implementation preserves the input order of equal elements in the sorted output. Mergesort is a divide and conquer algorithm that was invented by John von Neumann in 1945.
Algorithm
Conceptually, a merge sort works as follows:
- Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
- Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.
Top-down implementation
Example C-like code using indices for top down merge sort algorithm that recursively splits the list (called runs in this example) into sublists until sublist size is 1, then merges those sublists to produce a sorted list. The copy back step is avoided with alternating the direction of the merge with each level of recursion.
// Array A[] has the items to sort; array B[] is a work array.
TopDownMergeSort(A[], B[], n)
{
CopyArray(A, 0, n, B); // duplicate array A[] into B[]
TopDownSplitMerge(B, 0, n, A); // sort data from B[] into A[]
}
// Sort the given run of array A[] using array B[] as a source.
// iBegin is inclusive; iEnd is exclusive (A[iEnd] is not in the set).
TopDownSplitMerge(B[], iBegin, iEnd, A[])
{
if(iEnd - iBegin < 2) // if run size == 1
return; // consider it sorted
// split the run longer than 1 item into halves
iMiddle = (iEnd + iBegin) / 2; // iMiddle = mid point
// recursively sort both runs from array A[] into B[]
TopDownSplitMerge(A, iBegin, iMiddle, B); // sort the left run
TopDownSplitMerge(A, iMiddle, iEnd, B); // sort the right run
// merge the resulting runs from array B[] into A[]
TopDownMerge(B, iBegin, iMiddle, iEnd, A);
}
// Left source half is A[ iBegin:iMiddle-1].
// Right source half is A[iMiddle:iEnd-1 ].
// Result is B[ iBegin:iEnd-1 ].
TopDownMerge(A[], iBegin, iMiddle, iEnd, B[])
{
i = iBegin, j = iMiddle;
// While there are elements in the left or right runs...
for (k = iBegin; k < iEnd; k++) {
// If left run head exists and is <= existing right run head.
if (i < iMiddle && (j >= iEnd || A[i] <= A[j])) {
B[k] = A[i];
i = i + 1;
} else {
B[k] = A[j];
j = j + 1;
}
}
}
CopyArray(A[], iBegin, iEnd, B[])
{
for(k = iBegin; k < iEnd; k++)
B[k] = A[k];
}
Bottom-up implementation
Example C-like code using indices for bottom up merge sort algorithm which treats the list as an array of n sublists (called runs in this example) of size 1, and iteratively merges sub-lists back and forth between two buffers:
// array A[] has the items to sort; array B[] is a work array
void BottomUpMergeSort(A[], B[], n)
{
// Each 1-element run in A is already "sorted".
// Make successively longer sorted runs of length 2, 4, 8, 16... until whole array is sorted.
for (width = 1; width < n; width = 2 * width)
{
// Array A is full of runs of length width.
for (i = 0; i < n; i = i + 2 * width)
{
// Merge two runs: A[i:i+width-1] and A[i+width:i+2*width-1] to B[]
// or copy A[i:n-1] to B[] ( if(i+width >= n) )
BottomUpMerge(A, i, min(i+width, n), min(i+2*width, n), B);
}
// Now work array B is full of runs of length 2*width.
// Copy array B to array A for next iteration.
// A more efficient implementation would swap the roles of A and B.
CopyArray(B, A, n);
// Now array A is full of runs of length 2*width.
}
}
// Left run is A[iLeft :iRight-1].
// Right run is A[iRight:iEnd-1 ].
void BottomUpMerge(A[], iLeft, iRight, iEnd, B[])
{
i = iLeft, j = iRight;
// While there are elements in the left or right runs...
for (k = iLeft; k < iEnd; k++) {
// If left run head exists and is <= existing right run head.
if (i < iRight && (j >= iEnd || A[i] <= A[j])) {
B[k] = A[i];
i = i + 1;
} else {
B[k] = A[j];
j = j + 1;
}
}
}
void CopyArray(B[], A[], n)
{
for(i = 0; i < n; i++)
A[i] = B[i];
}
Top-down implementation using lists
Pseudocode for top down merge sort algorithm which recursively divides the input list into smaller sublists until the sublists are trivially sorted, and then merges the sublists while returning up the call chain.
function merge_sort(list m)
// Base case. A list of zero or one elements is sorted, by definition.
if length of m ≤ 1 then
return m
// Recursive case. First, divide the list into equal-sized sublists
// consisting of the first half and second half of the list.
// This assumes lists start at index 0.
var left := empty list
var right := empty list
for each x with index i in m do
if i < (length of m)/2 then
add x to left
else
add x to right
// Recursively sort both sublists.
left := merge_sort(left)
right := merge_sort(right)
// Then merge the now-sorted sublists.
return merge(left, right)
In this example, the merge function merges the left and right sublists.
function merge(left, right)
var result := empty list
while left is not empty and right is not empty do
if first(left) ≤ first(right) then
append first(left) to result
left := rest(left)
else
append first(right) to result
right := rest(right)
// Either left or right may have elements left; consume them.
// (Only one of the following loops will actually be entered.)
while left is not empty do
append first(left) to result
left := rest(left)
while right is not empty do
append first(right) to result
right := rest(right)
return result
Bottom-up implementation using lists
Pseudocode for bottom up merge sort algorithm which uses a small fixed size array of references to nodes, where array[i] is either a reference to a list of size 2 i or 0. node is a reference or pointer to a node. The merge() function would be similar to the one shown in the top down merge lists example, it merges two already sorted lists, and handles empty lists. In this case, merge() would use node for its input parameters and return value.
function merge_sort(node head)
// return if empty list
if (head == nil)
return nil
var node array[32]; initially all nil
var node result
var node next
var int i
result = head
// merge nodes into array
while (result != nil)
next = result.next;
result.next = nil
for(i = 0; (i < 32) && (array[i] != nil); i += 1)
result = merge(array[i], result)
array[i] = nil
// do not go past end of array
if (i == 32)
i -= 1
array[i] = result
result = next
// merge array into single list
result = nil
for (i = 0; i < 32; i += 1)
result = merge(array[i], result)
return result
Lets have a look on the actual code :



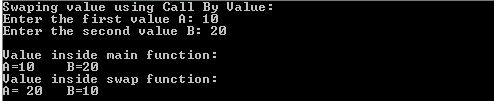
Comments
Post a Comment